Matematika tanár: "Volt néhány furcsa meglepetés az idei középszintű matekon"
Matematika érettségi 2024.

Azt előre lehetett tudni, hogy az idén változik a matematika érettségi, de ami igazán meglepetést jelentett, az az, hogy nem úgy változott, ahogy a NAT2020.
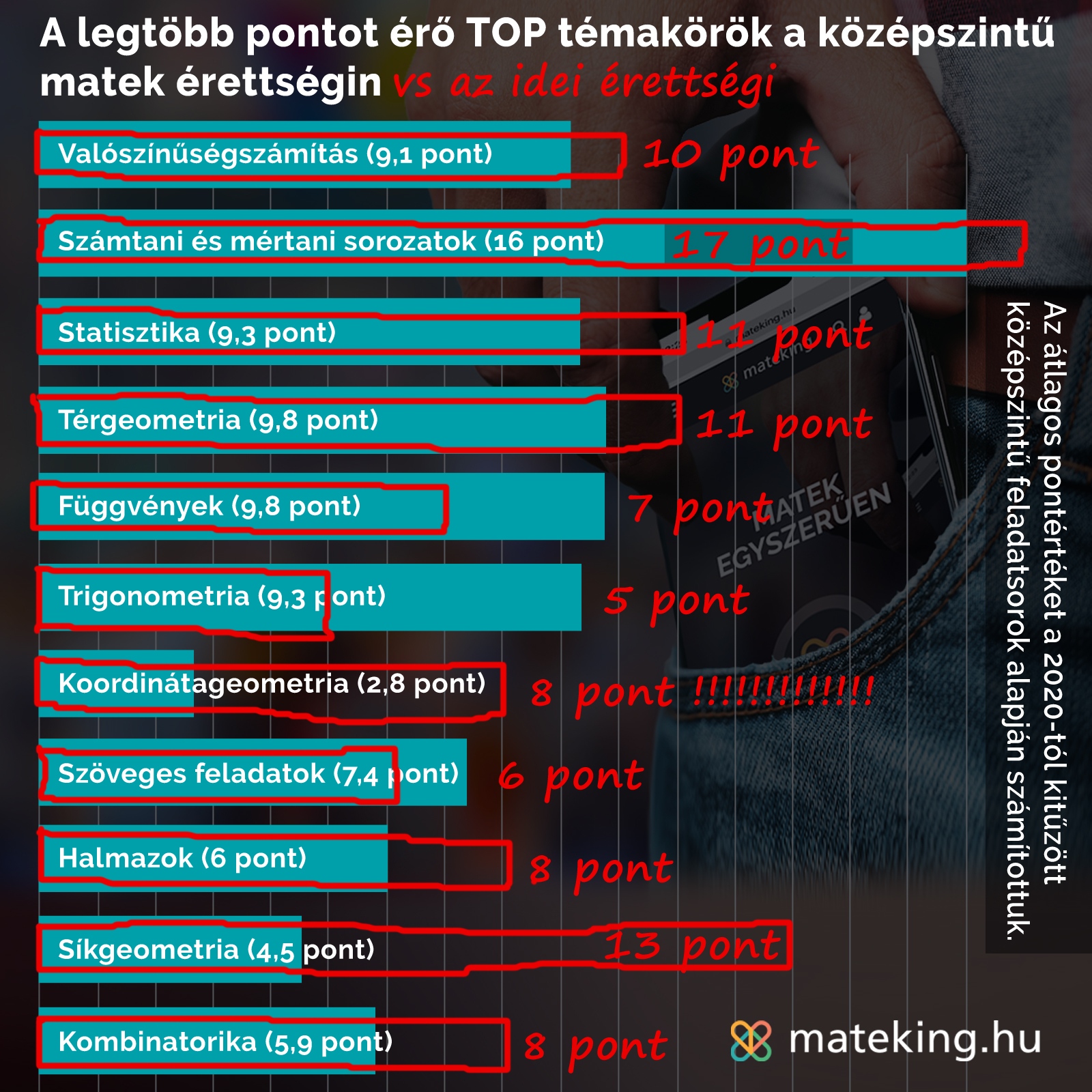
Az új témakörök, mint a kamatos kamat, várható érték, geometria valószínűség egyáltalán nem fordultak elő az érettségi feladatsorban. Egyedül a statisztika témakörben jelent meg a két előre beharangozott téma: a box plot és a “csaló grafikonok leleplezése”, amelyek 2 pontot és 4 pontot értek.
Vagyis 6 pontnyi új téma volt.
Ennél is nagyobb meglepetés viszont, hogy a másodfokú egyenletrendszerek deklaráltan kikerültek a középszintű követelmények közül, mégis szerepelt az idei érettségiben
– igaz egyetlen lépéssel vissza lehetett vezetni sima másodfokú egyenletre. Ez egyébként a 16. feladat c) része 8 pontért.
További furcsaság, hogy mindez egy koordinátageometria feladatban szerepelt. A koordinátageometria témakör követelményeit éppen a 2020-as NAT nyirbálta meg jelentősen. Bár magának a konkrét feladatnak a megoldásához a kör egyenletének a felírására elegendő volt, és ez továbbra is követelmény, a gond itt nem is ez.
A gond ezzel a feladattal az, hogy nagyon leegyszerűsítve de mégis egy kör és egyenes metszéspontjainak kiszámolását kéri. Márpedig ez deklaráltan nem középszintű anyag.
Sem a kör és egyenes metszéspontja, sem annak a másodfokú egyenletrendszernek a megoldása, amire szükség van a feladat megoldásához.
Skizofrén helyzet, hogy évek óta nem szerepelt ilyen típusú számításokat igénylő koordinátageometria feladat az érettségin, és erre most, hogy ezek már hivatalosan kikerültek a követelmények közül, most igen.
Szintén nem szokványos az érettségi 13. feladata, ami lényegében a 8. osztályos gimnáziumi felvételiben is szerepelhetett volna. Elsőfokú zárójeles egyenletet kellett megoldani, és két szám prímtényezős felbontását és a számok közös osztóit.
Ezek nem érettségibe való feladatok, hacsak nem az a célja, hogy tesztelje mennyit felejtettek a diákok 8. osztály óta a gimnáziumban.
A 14. feladat első része is szerepelhetett volna a gimnáziumi felvételiben, és a többi rész is elég könnyen megoldható korrekt feladat volt.
A 15. feladat is teljesen korrekt és könnyű volt, mint ahogy a 16. feladat is, leszámítva a skizofrén részfeladatot a kör és egyenes metszéspontjával.
A 17. feladatban újra egy skizofrén helyzet alakul ki amikor a c) kérdésben egy olyan valószínűséget kérdeznek, ami lényegében binomiális eloszlás és ez szintén kikerült a középszintű követelmények közül. Természetesen kijön binomiális eloszlás nekünk is, de ez a feladat is feszegeti a határokat.
Gond itt sem a feladat nehézségéből adódik, hanem abból, hogy miért pont akkor szerepel egy ilyen feladat az érettségiben, amikor deklaráltan épp most került ki az a képlet a középszintű követelmények közül, amellyel ezt a feladatot rutinszerűen meg lehet oldani.
Összességében a skizofrén helyzeteket leszámítva ez egy könnyű érettségi volt, egy biztonsági játék az összeállító bizottság részéről.


Fotók a cikkben: Győr, 2024. május 7. Diákok a matematika írásbeli érettségi vizsgán a győri Kazinczy Ferenc Gimnázium és Kollégiumban. MTI/Krizsán Csaba